Maya:mia_material_part05
Let’s start where we left off last time ●Bump The bump input accepts a shader that perturbs the normal for bump ma […]
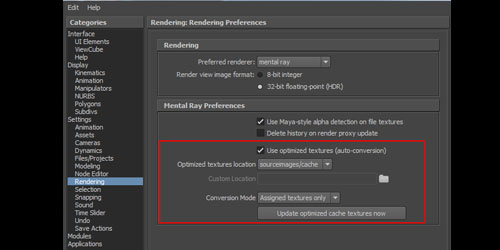
テクスチャが重すぎてレンダリングできないっ、って時に以下の設定をしてテクスチャを最適化すると解決するかも。テクスチャサイズはでかくなる一方ですし。プリファレンスから設定します。Windows -->> Setting/Preferences -->> Preferences -->> Rendering 上の画像の赤枠の部分。『Use Maya-style alpha detection on file texture』にチェックを入れます。(2012ではデフォルトOFF)この状態でレンダリングをするか、下の"Up[...]
read more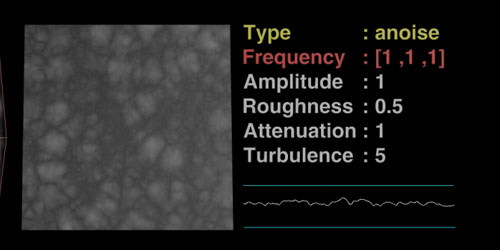
Houdiniです。Turblent Noise(VEX)についてのざっくりあれこれ。Frequency・・・周波数、値を大きくすると模様が細かくなる。Offset・・・オフセット。スライドさせる、的な。Amplitude・・・振幅の大きさRoughness・・・粗さAttenuation・・・コントラストっぽいのTurblence・・・ノイズの反復以下は、Volumeは3D noiseを、Planeは2D noiseを、Lineは1軸にnoiseを適応したものです。Perlin NoiseWiki曰く、「疑似乱数的な見た目で[...]
read more
Houdiniノード勉強回。今回は、"POP Proximity DOP"ノード。見たことあるけど使ったことないノード。Proximityとは日本語で「近接」を意味する言葉です。つまりPOP Proximity DOPはパーティクルの近接ポイントに関する情報を生成してくれるノードです。ほとんど使ったことないノードだったのですが実際に使ってみると、意外と有用なノードかもという印象。食わず嫌いはよくないなと。反省。こんな感じに、POPネットワークに組み込むと、nearest, nearestdist, numproximityといったアト[...]
read more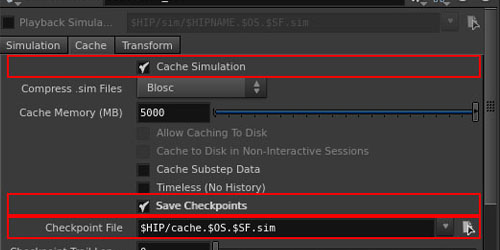
今回は、シミュレーションを途中から再開する方法です。これを使えば、エラー等でシミュレーションが止まった場合でも、最初からやり直しせずにすみます。途中からシミュレーションをするには、”シミュレーションキャッシュ”というものが必要です。DOP Networkノードに設定項目があります。1:シミュレーションキャッシュを有効にするDOP Networkにある、"Cache Simulation"を有効にします。2:シミュレーションキャッシュを保存する。"Save Checkpoints"を有効にします。"Checkpoint File"でシミュレーション[...]
read more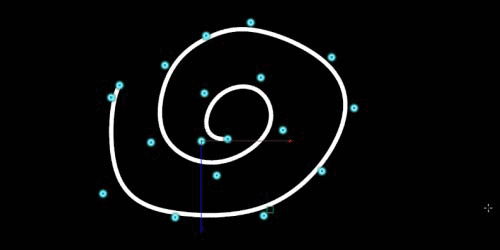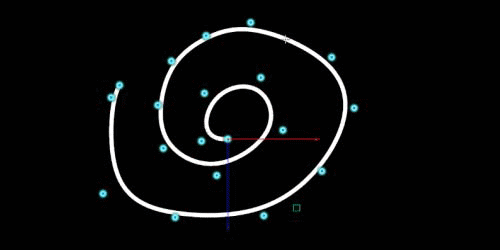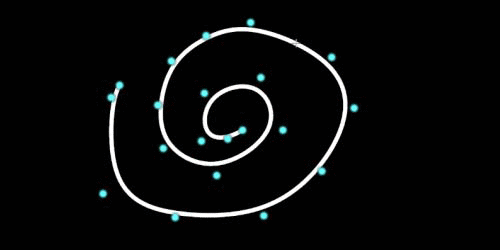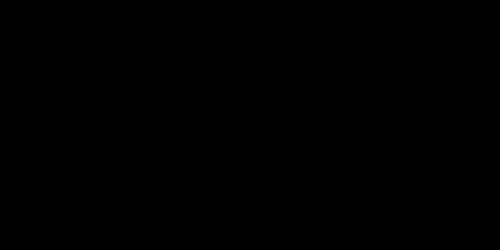
Houdini回Cureve(SOP)で、あとからコントロールポイントを増やす方法が分からなかったので調べた。答えは、カーブを選択してEnter! & Shiftを押しながら、クリック!途中にポイントを挿入することも、端点からカーブを伸ばすことも出来ました。わざわざ調べたのですが、よくよく見るとView上に書いてた。ちゃんと見なきゃだめですね。以上、また次回![...]
read more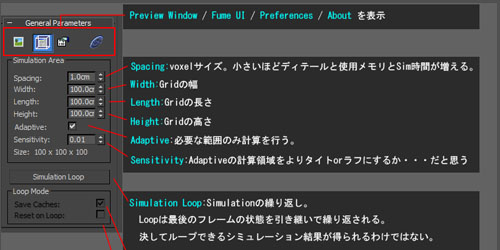
3dsMaxの流体プラグインFumeFXのメモを今回から数回に分けて公開します。改めてまとめてみると、いろいろ発見があるものですね。今回は作成時のパラメータメモバージョンは3.5です。<General Parametersロールアウト><Viewport ロールアウト>●ショートカット: = FumeFX UIを表示する間違い等ありましたら、ご指摘いただけると助かります。その1 ?,その2 ,その3 ,その4 ,その5, その6, その7, その8, その9RayFireのパラメータ意訳メモ[...]
read more
『miss_fast_skin_maya』の続きです。 Subsurface Scattering LayerBack Scatterはオブジェクトの背後から透過してくる光の効果とでも言いましょうか。太陽に手をかざしたときに輪郭が透けて見えるあれです。なので、オブジェクトの向こう側に光源を置く必要があります。バックライトというやつですね。Back Scatter Color透過してきた光の色かな。Back Scatter WeightBackScatterのウェイト。EpidermalとかSubdermalのとこのWeightと同じですね。この値[...]
read more
Maya回。Arnoldでレンダリングした際、aiSkyDomeLightがレンダリングされてしまって困った。こんな感じ。デフォルトではライトの白色が背景色のようにレンダリングされている。ここで見ると、背景白だから分かりにくいけど、キャラの後ろにライトの白が映っている状態。aiSkyDomeLight自体はレンダリングされず、ライティングにのみ影響してほしい。こんな感じに。そのためには、ShapeノードのAttribute Editorで"Visibility"の項目にある、Cameraの値を0にするらしい。最近の仕様らしい。教え[...]
read more
またtoxik回です。ニーズが多くないのは知ってるんですけどねぇ~。今回はPXLノード。"PXL"とはPixel eXpression Languageの略だそうです。(頭文字ってわけじゃないのね)ひとことで言うと、スクリプト書いたらピクセル単位で絵を操作できるよ”っていうノードです。なのでプログラム&算数の知識が要求されます。たとえば、AEでいうフラクタルノイズなんかはコレで作れます。実は、『Toxikでフラクタルノイズ作るにはどうしたらいいですかね』って質問したら、『これ使えばいいよ』って教えてもらったのです。しかしExpression書[...]
read more
Lightstorm3Dの無料ツールライブラリ「L3Library」にある機能の一つ、GeoLocatorが面白かったので備忘録も兼ねて。GeoLocatorという機能は、どうやらコンストレイン+追従の動きにノイズやDynamicsを加味するというものらしいです。試しに作ってみました。まず、インストール方からざっくりと。①サイトからL3Libraryをダウンロード。(※登録必要)②任意の場所にファイルを解凍。③Maya起動④ScriptEditorを起動しPythonタブに切り替え、↓のスクリプトをコピー&ペースト[...]
read moreLet’s start where we left off last time ●Bump The bump input accepts a shader that perturbs the normal for bump ma […]
Let’s start where we left off last time ●Indirect Illumination Options ・FG/GI Multiplier An indirect multiplier th […]
Let’s start where we left off last time ●Anisotropy ・Anisotropy Sets the ratio between the width and height of the […]
Let’s start where we left off last time ●Refraction ・Index of Refraction The amount that a ray of light bends when […]
I checked and summarized “mia_material” Although there was a blank part of the knowledge which has not yet b […]




