前回に引き続き、「内積」についてです。
内積を上手に使うと、角度を知ることができます。
今回は、その辺りに焦点を絞って書いてみたいと思います。
また、3DCGでは、角度を知るために内積が沢山使われています。
後半でその辺りの簡単な活用例をいくつか取り上げたいと思います。
が、その前に!
ここで内積についての情報を少々。
内積のことをスカラー積とも呼びます。
これは内積の計算結果がスカラー値になるからだと思われます。
スカラー値ってのは普通の数のことです。
ベクトルが複数の値で構成され、向きや速度、大きさといったものを同時に表すのにたいして、単に大きさや量を表すものとして、単一の値で構成されたものをスカラー値と呼びます。
また、内積は英語ではdot productと表記されています。
内積の計算記号が ・ だからでしょうか?
3DCGやプログラムではこちらの表記の方が馴染み深いかと。
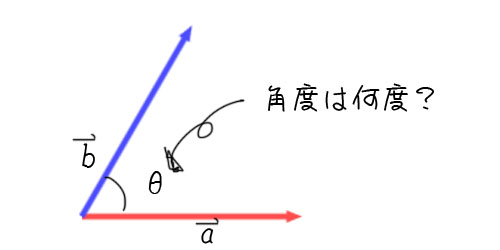
では内積の角度についての特性を見ていきましょう。
まず、結論から。
単位ベクトルどうしの内積を計算すると、そのベクトルの成す角度がわかります。
単位ベクトルどうしというのがミソです。
ちなみに単位ベクトルとは長さが1のベクトルのことです。
また、任意のベクトルを単位ベクトルに変換することを正規化(normalize)といいます。
もそっと詳しく。
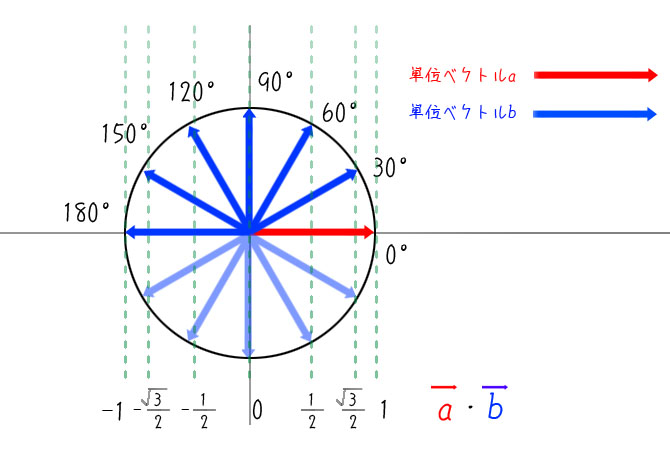
単位ベクトルどうしの内積を計算すると、1~-1の値が得られます。
この値は0°~180°に対応しています。
なので内積の値がわかると0°~180°の範囲で角度がわかるのです。
たとえば、内積の値が1の場合、ふたつのベクトルは同じ方向を向いていることを意味します。
-1だと反対方向を向いている事を意味します。
0だと90°で直交というわけです。
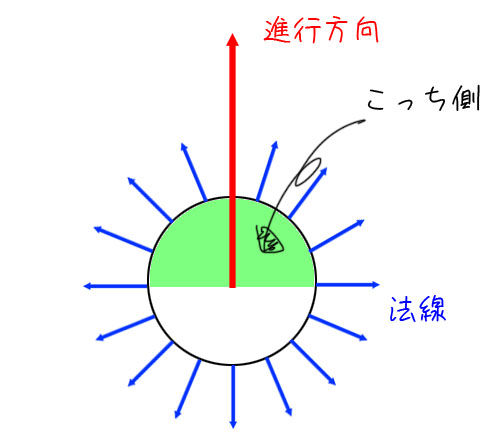
(図1は、ベクトルaを可変、ベクトルbを固定した時の角度と内積の関係を書いたつもり)
「図1」
なぜそういえるのか?
数式の側面から考えてみます。
いきなり三次元のベクトルは(私が)混乱するので、二次元ベクトルの内積で考えます。
まずは内積の定義式をおさらいします。
ベクトルa、bがそれぞれ長さが1のベクトル(以下、単位ベクトルと表記)の場合、上記の内積の定義式は次のように変形できます。
単位ベクトルの内積はcosθに相当します。
cosθのとりうる範囲は1~-1でそれは0°~180°に相当します。
つまりcosθの値が分かるということは、それに対応する角度θが0°~180°の範囲でわかる、ということです。
∴単位ベクトルの内積を求めると角度がわかる!
さて、角度θを知るには単位ベクトルの内積を計算すればよいことがわかりました。
前回やりましたが、内積はベクトルの各成分からも求めることができます。
これです。
つまり、単位ベクトルの各成分を掛けて足せば角度がわかる、ということです。
ベクトル成分の、掛け算と足し算で角度が分かるというのは結構すごいことだと思います。
ここでは二次元ベクトルで考えましたが、三次元ベクトルでも考え方は同じです。
この内積を使った角度を知る方法は、3DCGの世界でいろいろ使い道があります。
幾つか例を上げてみようとおもいます。
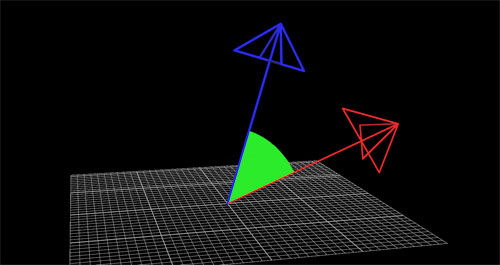
【例1】

(Houdini File:Dot_sample_001)
反対側からはパーティクルは発生してません。
進む向きが変わると、発生する場所も変わります。
別な言い方をすると、”進行方向に対して0°~90°の角度”の法線を持つ面からパーティクルが発生している”、とも言えます。
この、”進行方向に対して0°~90°の角度”の判別に内積を利用しています。
オブジェクトの進行方向ベクトルと、ポリゴンの法線ベクトルの内積を求めれば、進行方向に対してポリゴンがどの方向に向いているか-1~1の値でわかります。
得られた結果の0~1の範囲が0°~90°の範囲に該当します。
つまりポリゴンが進行方向側を向いている事を意味します。
上の例は、そうやってパーティクルの発生元を決定しています。
利用する内積の範囲を変えれば、任意の角度でパーティクルの発生源が調整可能です。
もひとつ!
【例2】
【例2】はカメラから見て0°~90°の角度で面にグラデーションを付けています。
これも内積を使ってます。
同じ絵はほとんどの3DCGソフトで標準で作れます。
MayaだとSamplarInfoのFacingRatioで、3dsmaxだとフォールオフで、HoudiniだとNormal Falloff(VEX)あたりでできるかと。
これらは内部で、法線ベクトルとカメラの向きベクトルをそれぞれ正規化し内積を計算、その値に応じて色をマッピングしているのだと思います(たぶん)。
ちなみに、例2はHoudiniで作ったものです。(Houdini File:Dot_sample_002)。
他にもToon系シェーダのライン描画はエッジ検出に内積使ってるはずですし、
大概のシェーダはDiffuse等の計算にはライト方向と法線の内積を使っているのではと想像します。
この内積を使った角度の調べ方は、私も仕事で時々使います。
便利です。
と、こんな感じに内積は3DCGの世界でいろいろと使われているのでした。
今回はこのくらいで。
次回は内積を使った大きさの求め方(?)について書きたいと思います。
おかしなところがありましたらこっそり教えてください。
しれっと直します。
(あまり関連ない記事:arctan2(アークタンジェント2)ってなんぞ?)
参考サイトURL
wiki:単位ベクトル
ベクトルの内積とは
http://blog.livedoor.jp/akinow/archives/52297066.html
http://www.deqnotes.net/acmicpc/2d_geometry/products
http://www.wakayama-u.ac.jp/~wuhy/am2.pdf
http://www.soft-syokunin.com/?p=788
他たくさんのサイトを参考にさせていただきました。

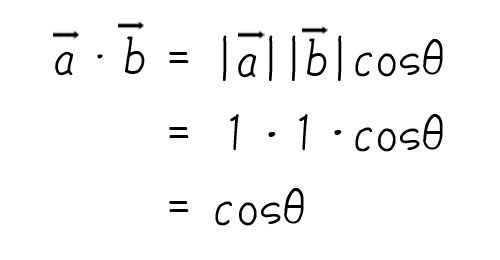












コメント