前回に引き続き、内積についてです。
前回は内積を使って角度を知る方法についてでしたが、今回はベクトルの大きさについてです。
内積を上手に使うと、任意のベクトルが別のベクトルに落とす影の大きさを知ることができるのです。
・・・なんのこっちゃですかね。
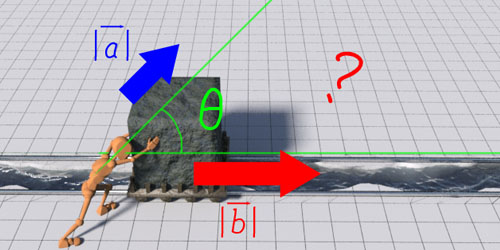
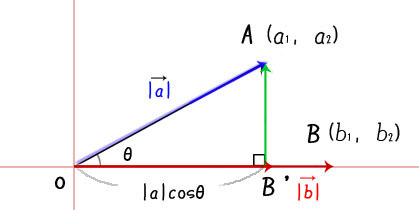
初回のトロッコの例で、斜めに押す力(ベクトルa)の中にトロッコを動かす力(ベクトルb)がどれだけ含まれているかを求めました。cosを使って|a|cosθでしたね。
この|a|cosθの値を知りたい時にも内積が使える、そういうことです。
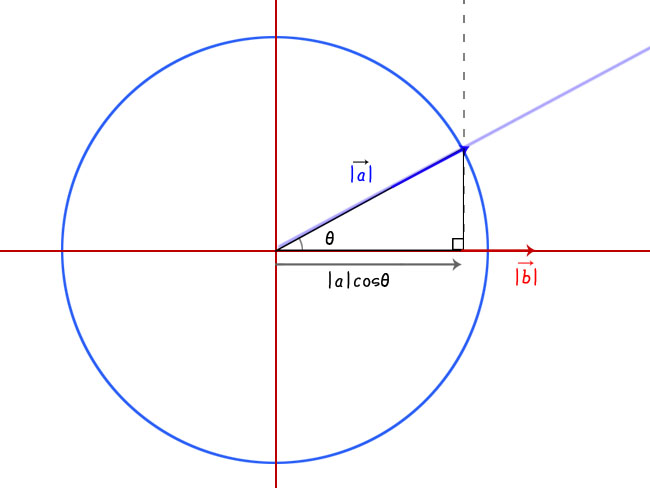
内積の定義式は、|a||b|cosθでしたね。
ここで、ベクトルbが大きさ1のベクトル(単位ベクトル)だった場合を考えてみます。
内積の式はこう書けます。
内積はベクトルの各成分を掛けて足すことでも求められます。
おさらいすると、内積はベクトルの各成分を使って、このように定義されます。
つまり、正規化してないベクトルaと、正規化したベクトルbの各成分を掛けて掛けて足せば、|a|cosθが求められる、と。
この|a|cosθとはなんじゃ?
最初に書きました通りこれは、あるベクトルが別の単位ベクトルに落とす影の大きさと見ることができます。
また違う見方をすると、あるベクトルに含まれる任意の単位ベクトル方向の成分とも言えるかもしれません。
さて、こんなもの求めてどうすんじゃ?、と思うかもしれませんが、案外使い道があるものです。
3DCGでの例ですが、以前このサイトで車輪のリグについて考察した時、この内積の特性を利用しました。
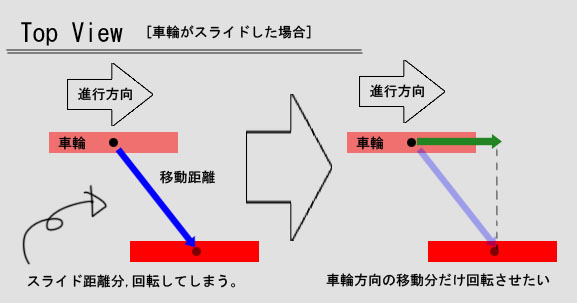
これは、車輪の移動距離と回転角を連動させて、正確に車輪の移動分だけ回転させる仕組みにしたもです。
一見うまく動いてるっぽいですが、問題がありました。
車輪が横にスライドした場合にもその移動距離分車輪が回転してしまうのです。
その対策として内積を使ってみました。
内積を用いて移動ベクトルから車輪の向いている方向のベクトルの大きさを求め、その分だけ車輪を回転させるようにしました。
これで、一応は車輪が横滑りした際にも、過剰に回転することはなくなりました。
あまり、よい例じゃないかもしれませんが、ともかく使い道はありました、と。
あと、一度も使ったことないけど、自分自身の内積をとると、絶対値を計算するのと同じ結果が得られます。
さて、内積について3DCGと絡めて、数回に分けて書いてみましたが、それもここまで。
内積についてというよりは、内積の活用法だったかもしれませんね。
もっと知りたいという方にとっては物足りない内容だったかもしれませんが、CG屋としてはこれで必要十分と思った次第です。
(内積空間とか手に負えませんし)
何か書き忘れがあったら、追記します。
ともかく、お疲れ様でしたm(_ _)m
おかしなところがあったら、こっそり教えてください。
しれっと直します。
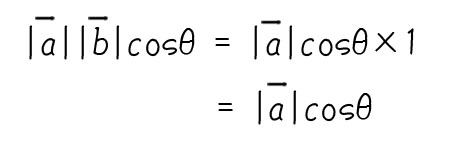

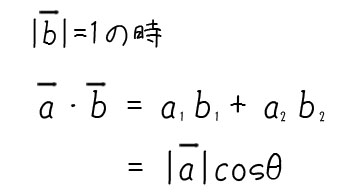







コメント