No More Retake

今回はちょっと変わったネタを。
極座標変換についてです。半分、数学です。

極座標系とは、ザックリ言うと”角度(θ)”と”距離(r)”で表される座標の事です。
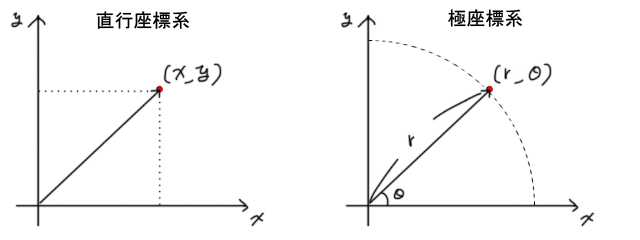
下に二次元の直交座標系と極座標系の図を載せてみました。

図のように、同じ座標でも直交座標と極座標という二つの方法で表すことが出来きます。
同じ一つの場所を異なる座標系で表すことが出来るというのは、時として非常にありがたいことだったりします。
直交座標ではややこしい制御も、極座標ならすんなりなんてこともあるかもしれませんからw
この、直交座標系と極座標系を行き来するためには、変換式が必要になります。
難しい話は、参考URL参照にして、上図の極座標直と交座標の変換式を書くとこうなります。

#極座標→直交座標
x = r cosθ
y = r sinθ

上式は、極座標[r,θ]→直交座標[x,y]への変換式です。
距離と角度から位置を求めていると言っても良いですね。
（直交座標[x,y]→極座標[r,θ]への変換式も載せたいとこですが、書式の関係で割愛します。
興味と時間のある方は自分で導き出してみてはいかが？
上記の図からも導き出せます。
ヒントは、三平方の定理とアークタンジェントです）

ここまでの極座標系の話は二次元でしたが、三次元でも同様です。
つまり、[X,Y,Z]の直交座標を、[r, θ,φ]の極座標で表すことが出来るのです、
(rは距離、θ、φは角度)Mayaでサンプルを作成してみました。
下記pymelを実行するとサンプルシーンが作成されます。

import pymel.core as pm

#box作成
oObj = pm.polyCube(n="Cube_GEO")[0]

#アトリビュートを追加（半径）
oObj.addAttr( "R" ,at="float", dv=5)
oObj.setAttr( "R" ,k=1)

#アトリビュートを追加（角度）
oObj.addAttr( "V_rad" ,at="float", dv=0)
oObj.setAttr( "V_rad" ,k=1)
oObj.addAttr( "H_rad" ,at="float", dv=0)
oObj.setAttr( "H_rad" ,k=1)
#不要なアトリビュートを非表示
oObj.setAttr( "translateX" ,k=0)
oObj.setAttr( "translateY" ,k=0)
oObj.setAttr( "translateZ" ,k=0)
oObj.setAttr( "rotateX" ,k=0)
oObj.setAttr( "rotateY" ,k=0)
oObj.setAttr( "rotateZ" ,k=0)
oObj.setAttr( "scaleX" ,k=0)
oObj.setAttr( "scaleY" ,k=0)
oObj.setAttr( "scaleZ" ,k=0)
oObj.setAttr( "visibility" ,k=0)

#box作成
oObj2 = pm.polySphere(n="temp_GEO")[0]
oObj2Shape = oObj2.getShape()
print oObj2Shape.radius.get()

expName = "Polar_coordinates"
exp = "$r = Cube_GEO.R;n"
exp += "Cube_GEO.translateX = $r * sin(Cube_GEO.V_rad) * cos(Cube_GEO.H_rad);n"
exp += "Cube_GEO.translateY = $r * cos(Cube_GEO.V_rad);n"
exp += "Cube_GEO.translateZ = $r * sin(Cube_GEO.V_rad) * sin(Cube_GEO.H_rad);n"

pm.expression(string = exp,  name = expName)

pm.cycleCheck( e=0)

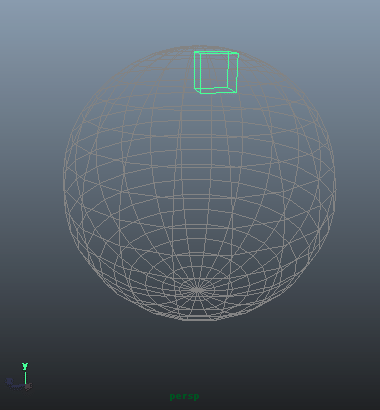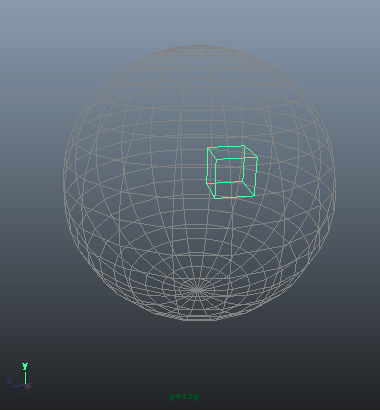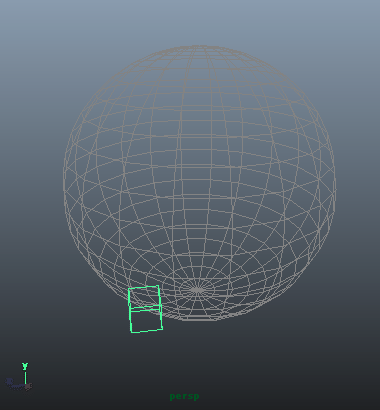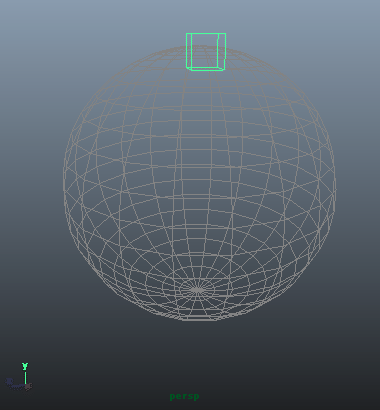
実行すると、立方体が一個作成されます。
パラメータは３つ。
中心からの距離：R、縦の角度：V_Rad、横の角度：H_Rad。
このうち、V_RadとH_Rad、二つの角度のパラメータをぐりぐりと変更して立方体を動かしたのがこちら。
このように、球面を滑るような動きになります。極座標系は円運動が得意なのです。

サンプルはMayaで作成しましたが、ソフト依存の知識ではないので使い方次第でいくらでも応用のきくものかと。

ちなみに、3次元の極座標→直交座標の変換式はこうなります。
時間と興味のある方はこの逆変換も考えてみてはいかが？

X = sinθ * cosφ
Y = cosθ?
Z = sinθ * sinφ

いろいろ駆け足で分かりづらい箇所もあったかと思いますが、結局何を言いたかったかというと、
「CG屋さんへ　極座標つかった制御方法ってのがあるよ」
これです。
極座標系については、他にも詳しく載っているサイトが多々ありますので興味のある方はそれらを回ってみるのも良いかと思います。

では、今回はこれにて。
間違い等ありましたら是非ご指摘を！

参考URL
http://www.kkaneko.com/rinkou/octave/coordinates.html
http://lasbim.taiiku.tsukuba.ac.jp/VSB/04/0402.html
http://www.mvision.co.jp/WebHelpIM/_RESOURCE/Filter_Mvc_Polar.html

http://tau.doshisha.ac.jp/~kon/lectures/2005.calculus-II/html.dir/node30.html
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1476428324
http://ft-lab.ne.jp/cgi-bin/wiki.cgi?page=%C6%C8%A4%EA%B8%C0%C6%FC%B5%AD%A1%CA2008%2F06%A1%CB