今回は少し趣向を変えて、数学の話です。
ですが、その前に
= 注意 =
大丈夫!という方は用法用量を守って適当にお読み下さい。
タイトルにあるとおり、arctan2(アークタンジェント)とはなんぞやです。
アークタンジェントってなんぞや。タンジェントじゃないんか?
2ってなんぞや? 1があるんか?
3DCGの作業で何に使えるのぞや?
管理人の復習もかねてまとめてみました。
前半部ではMayaでの使用例を交えたプログラム的な解説。
後半部では数学的な解説、とわけて書きます。
文字多めで、記事長めですがご容赦を。
atan(アークタンジェント)とはtan(タンジェント)の逆関数のことです。
三角関数の類ですね。
プログラムではatanと表記されることが多いです。(以下arctanをatanと表記します)
はて逆関数とは?、という疑問はいったん飲み込んで、進みます。
このatanを使うと何ができるのかというと、tan(タンジェント)の値が分かれば角度を求めることができます。
tan(タンジェント)というのは底辺と高さの比なので、この二つの長さが分かれば角度が求められるということです。
MayaのMELにもatan()関数があるので、実際に使ってみます。
$rad = atan(1); $deg = rad_to_deg($rad); print $deg; //結果 45
上記MELでは、一行目でtanの値が1に対応する角度をatan()関数を使って求めています。
atan()で求められる角度はラジアン(弧度法)なので、それを馴染みのある”度”に変換しているのが二行目。三行目でその結果を表示しています。タンジェント45度の値は1なので、結果はあってます。
atanは角度を求めたい時に非常に役立つものなのです。
角度が分かればタンジェントの値を求められるのがtanで、タンジェントの値が分かれば角度が求められるのがatanというふうに見ればなんとなく逆関数のイメージが見えてくるのでは。
大概のプログラム言語は三角関数が扱えるので、このatanを扱う関数が存在します。
C++、javascript、python等。もちろんMayaのMELしかり、3dsMaxのMaxScriptしかりです。
しかし、tan(タンジェント)の値なんてものは、そのへんに転がっている類のものではありません。求める必要があります。それじゃあちょっと使いづらいよね、ってことで用意されたのがatan2なので(はないかと思っていま)す。
つまり、atan2とはatanをより使いやすく拡張した関数と言えます。
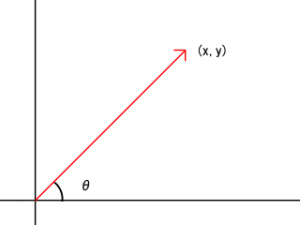
では、どのように機能拡張されたのかというと、このatan2、ベクトル(座標)を与えると、そのベクトルとX軸の成す角度を求めてくれます(下図、角度θ参照)。座標が分かれば角度が分かるのです。これは便利なのです。
これも、MayaのMELで試してみます。
$rad = atan2(sqrt(3), 1); $deg = rad_to_deg($rad); print $deg; //結果60
一行目でatan2()関数を使って角度を求めています。
このatan2()関数ですが、1番目の引数がY座標、2番目の引数がX座標となるので注意しましょう。sqrt()と関数を使っていますが、コレは平方根を求める関数です。ここでは√3です。
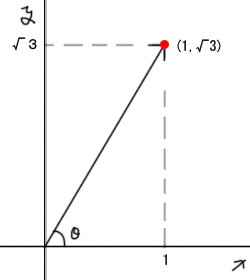
つまり一行目が言いたいことは、(X,Y) = (1,√3)の座標とX軸の成す角度を求める、です。
もう一つ作例をやってみます。
//cube作成 $cube = `polyCube -n CTRL`; xform -t 5 0 0; //矢印作成 curve -d 1 -p 0 0 -0.99 -p -0.66 0 0 -p -0.33 0 0 -p -0.33 0 0.66 -p 0.33 0 0.66 -p 0.33 0 0 -p 0.66 0 0 -p 0 0 -0.99 -k 0 -k 1 -k 2 -k 3 -k 4 -k 5 -k 6 -k 7 -n "controller1" ; xform -ro 90 0 -90; //Rotate制御用グループを作成、矢印を子供に group -n ROT -empty; parent controller1 ROT; //annotationを作成(ベクトル可視化用) spaceLocator -n "annotationLocator" ; xform -t 5 0 0; parent annotationLocator CTRL; annotate -tx "vec" annotationLocator; //expression実装 $expressionName = "Atan2_SampleExpression"; $exp = "$r = atan2d(CTRL.translateY, CTRL.translateX);"; $exp += "ROT.rotateZ = $r;"; expression -string $exp -name $expressionName;
上記MELを実行すると、同様のシーンが作成されるかと思います。
立方体の”CTRL”を動かすと、その方向に矢印オブジェクトが向くようになっています。(Z方向には対応していません)
MELの内容を軽く説明すると、
1~17行目までで、Boxや矢印といった必要なオブジェクトを作成しています。
18行目以降で、Expressionを作成して矢印の回転を制御しています。
Expressionの中身は単純で、atan2()関数で求めた角度を、矢印オブジェクトのRotateに代入しています。
また、ここではatan2()のかわりにatan2d()という関数を使っています。角度を度単位で求めてくれるのでラジアンからの変換の必要がないので使ってます。
他にも、atan2()はいろいろな局面で有効に働きます。
今後、当ブログで載せる予定の記事の中にもatan2()を使う予定のものがあったりします。
さて、なんとなくプログラム的なatan2()の使い方が分かったところで、頭を数学の方に切り換えます。
数学的にatan(アークタンジェント)とはなんぞや、逆関数とはなんぞや、といった方面について書いてみたいと思います。
そもそもtan(タンジェント)とはなんぞや?
ずばりtan = sin ÷ cos がタンジェントです。
なんのこっちゃですね。
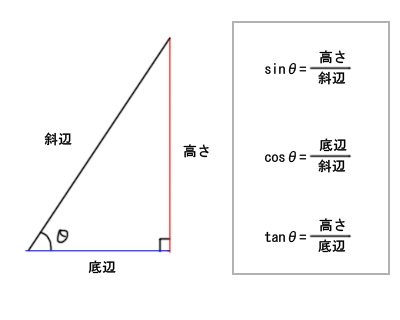
学校やなんかでは、直角三角形で、
sin = 斜辺÷高さで、cos= 斜辺÷底辺、tan = 底辺÷高さ、とか習うと思います。
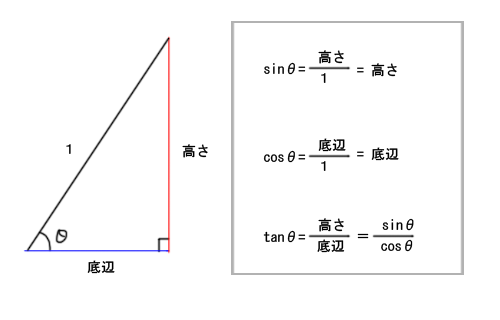
計算しやすいように斜辺が1の場合を考えてみます。(ベクトルで考えると正規化です)
斜辺が1の場合、sin = 高さ、cos=底辺となり、tan = 底辺÷高さ、から tan = sin ÷ cosが求められます。
言い換えると、sinθは高さ(y座標の値)を表し、cosθは底辺(x座標の値)を表し、tanθは底辺に対する高さの比(cosに対するsinの比)を表していると言えます。
ではこの底辺に対する高さの比とはいったい何でしょう?
答えは傾きです。
つまりtan(タンジェント)とは、どれだけ傾いているかの値といえるのです。
もう少し、具体的に考えてみましょう。
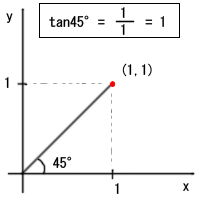
“tanθ= 1″の傾きとはどういう角度でしょう
底辺と高さの比率が1:1になるような傾きです。なんとなく想像がつきます。45°です。
初めのほうでatanとはtanの逆関数だと書きました。atanの定義はまさにそれ。
では逆関数とはなんぞや?
これが、なんとも説明しづらい。
上表でのθとtanθの関係を見ると、ある角度が特定のtanに対応するのなら、tanの値から角度が求められそうな気がしませんか?
tan()という関数が角度から傾きを求める関数だとすると、その逆の処理をして元の角度求める関数が逆関数、atan()といえます。
なんとなくでも、伝えられたでしょうか。
逆関数についてのさらなる思考は、難しいのでそうそうに止めました。
最後駆け足になりましたが、結局何が言いたかったかというと
「atan(アークタンジェント)を使うと座標から角度が得られて便利だよ」
ということです。
以上、お粗末でした。
間違い、勘違い等ありましたら是非ご指摘を!
参考URL
http://ja.wikipedia.org/wiki/%E4%B8%89%E8%A7%92%E9%96%A2%E6%95%B0
http://ja.wikipedia.org/wiki/%E9%80%86%E5%86%99%E5%83%8F
http://ja.wikipedia.org/wiki/%E5%82%BE%E3%81%8D_(%E6%95%B0%E5%AD%A6)
http://78578203.at.webry.info/201101/article_2.html
http://lowlife.jp/mft/stories/3.html
http://www.da-tools.com/AE/exp/jisen/atan.html
http://imax.iwa.hokkyodai.ac.jp/help/AppleWorks%20Help/fn/pgs/fntrigfn.htm#ATAN (Arc Tangent)









7年前の記事ですがグラフィックシェーダーで躓いている者です。
tanの説明大変参考になりました。