数学回です。
今回から、数回に分けて「内積」について書こうと思います。
が、その前に!
= 注意 =
この記事には三角関数やら数式やらが頻出します。
「三角関数は医者に止められてる」、というような方は読むのをお控えください。
また、一連の記事は、「内積がなんとなく分かった気になれて、3DCGで応用できそう」
くらいを想定しています。
数学として内積について深く掘り下げたものではありません。
玄人はサポート対象外です。
また、間違い等を見つけましたら、こっそりお知らせください。
おおっぴらに間違いを指摘されると、恥ずかしさで管理人が泣きます。
以上、あしからず。
「内積」と聞くと数学を連想すると思います。
実際に数学の類ですが、今回はその数学の類を物理の側面から眺めてみたいと思います。
唐突ですが内積の定義式から。
今は深く考えず、「へ~、これが内積の式ね」くらいに流していただければ。
昔の頭の良い人が、考えたんだなと。
最終的にはこの式が出てきます。
あと、三角関数についても少しおさらい!
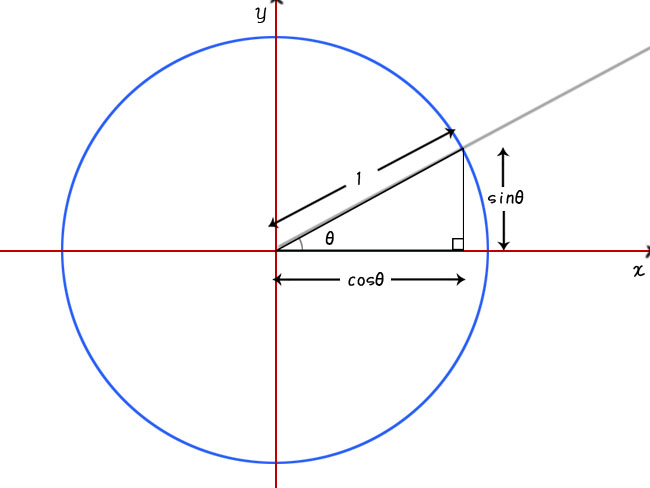
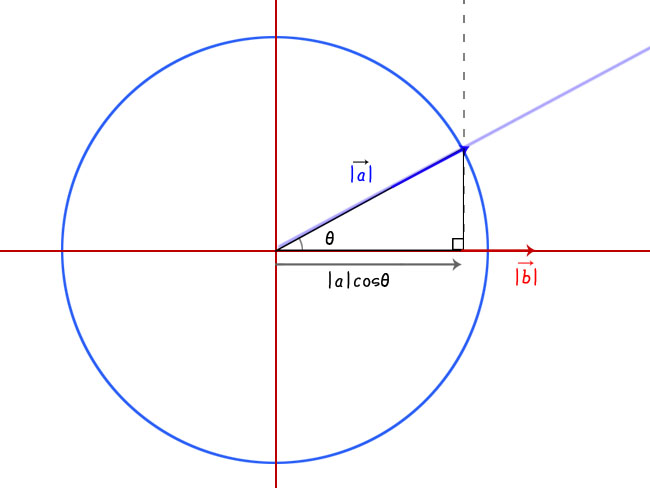
下図のような、斜辺が1の直角三角形を考えた時、底辺はcosθ、高さはsinθとなります。
ここで底辺のcosθに注目すると、cosθは斜辺がx軸へ落とす影のように見えますね。
この考え方をのちほど使います。
内積では特にcosθが頻出します。
では、本編スタート!
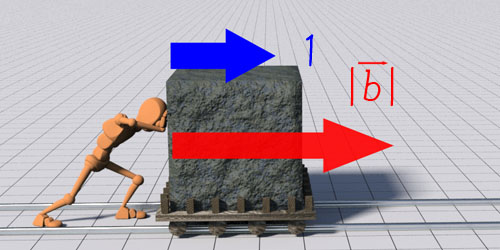
今ここに、1の力でまっすぐ押すと|b|進むトロッコがあるとします。
(ベクトルbの大きさを|b|とします)
1の力で|b|進むのならば、|a|の力で押すと|a|×|b|進む、っちゅうことです。
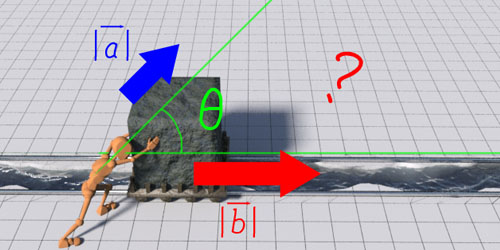
途中でまっすぐ押せなくなりました!
仕方がないので、斜めから押します。
トロッコの進む方向に対してθ°の角度で斜めから、|a|の力で押しました。
この時、トロッコはどれくらい進むのか?
これを計算できるのが内積です。
実際に考えてみましょう。
シンプルにするため、真上から見た平面(二次元)で考えます。
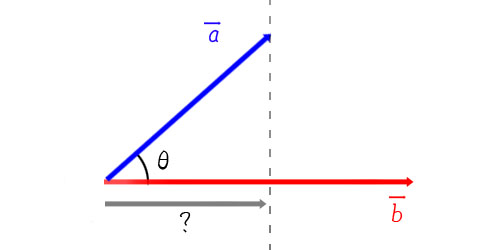
斜に押すわけですから、押す力すべてがトロッコを動かす力として使われるわけではなさそうですね。
まず押す力(ベクトルa)の中に、トロッコを動かす方向(ベクトルb)の力がどれだけ含まれているかを知る必要があります。
実はこれ、最初におさらいした三角関数を使うことで知ることができます。
知りたいのは上図の三角形の底辺にあたる部分なので、cosを使って|a|cosθと表せます。
ベクトルa(押す力)の中にはベクトルb方向(トロッコの進む方向)の力が|a|cosθだけ含まれているということです。
初めに書きましたが、このトロッコは1の力で押したら|b|進むトロッコです。
ならば|a|cosθの力で押した時、トロッコが進む距離は、
と、なります(交換則)
ほい!式の右辺にこのページの最初に見た内積の式が出現しました。
右辺に出てきたこの式を内積と定義し、記号 ・ を使って次のように書くことにします。
定義とは名前をつけるということ、言葉の意味を決めるということです。
なのでこの式の名前は内積です。
さて、実際にこの式を計算して内積の値を求めるにはどうすればよいでしょう?
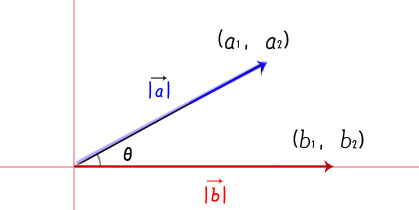
ベクトルa=(a1,a2)、ベクトルb=(b1,b2)としたとき、
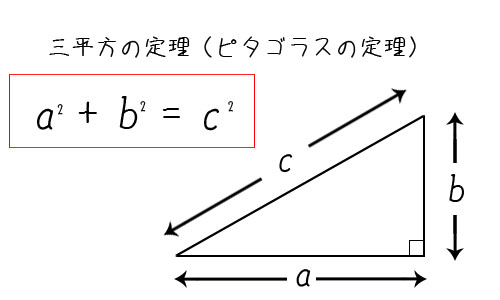
ベクトルの大きさ、|a|,|b|はそれぞれ三平方の定理で求められます。
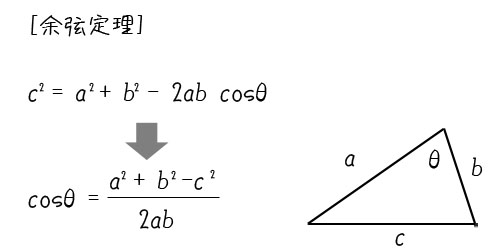
cosθは余弦定理を使って求められます。
最後にそれら、全部かけ合わせればおk。
ちなみに、三平方の定理は直角三角形の二辺の長さわかれば残り1辺の長さも求められるというものです。
余弦定理は、三角形の二辺の長さとその間の角度が分かっていれば、残り一辺の長さが分かるという定理です。
これらで求めた値を掛け合わせば内積の値が分かります。
でも、・・・計算がたくさん必要ですね。
・・・むずかしいですね。
実は、もっと簡単な計算方法があります。
これです。
掛けて、掛けて、足す。
内積はこの計算でも求められます。
ホントです。
先ほどチョロっと出た”三平方の定理”と”余弦定理”を使って、先の内積式を変形していくとコレになります。
ホントです。
では、実際に先の内積の式を変形させて確認してみましょう。
はい、先ほどの計算が出てきました。
これを計算すれば、|a||b|cosθを計算したのと同じ値を得ることができます。
内積を求める時は、こっちの方法を使う事がほとんどだと思います。
計算回数が少なくて済みますから。
これが三次元になっても考え方は同じです。
三次元でも三平方の定理、余弦定理は使えるので、同様の変形が可能です。
さて、ベクトル成分を掛けたり足したりすると、内積が求められることが分かりました。
これを上手に使うと、ベクトルの座標から向きを知ることができたり、特定成分を抽出したりといろいろ出来ることがあるのです!
実は、それらはものすごく便利でCG屋にも恩恵があるのです、が!
今回はここまで、続きは次回!
参考URL
http://naop.jp/topics/topics14.html
http://fnorio.com/0126scalar_&_vector_product/scalar_&_vector_product.html
http://www.sit.ac.jp/user/konishi/JPN/L_Support/SupportPDF/InnerProduct.pdf
http://hooktail.org/misc/index.php?%A5%D9%A5%AF%A5%C8%A5%EB%B2%F2%C0%CF
https://www.mathsisfun.com/algebra/vectors-dot-product.html
他多数。


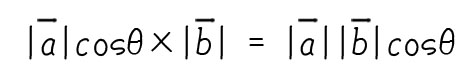
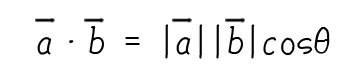
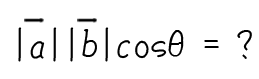














コメント