No More Retake
3DCG屋さん向けTips&Referenceサイト
-
Houdini:オモシロカタヨ
ネットワークこんな。勉強になった点retentionPolyReduce(SOP)のパラメータ"Retain Density by Attribute"を活用することで、任意の箇所を任意の割合でポリゴン数を削減出来る。デフォルトでは、"retention"というアトリビュートで、削減度合いをコントロール出来る。このアトリビュートを、Paint(SOP)でぬりぬりしながら、後工程の結果を見るのが楽しい。PolyExtrude(SOP)PolyExtrude(SOP)をうまく使うと、ポリゴンラインに幅を持たせて抽出する様な用途もイケる。[...]
続きを読む -
Houidniノード:if block(VOP)
Houdiniノード勉強回。今回はVOPのif block。"Block Begin If"と"Block End"ノードで構成される条件分岐のためのノード。「なんじゃこりゃ」、「どうやって使うんじゃ」と思って調べたやつ。・・・VimeoのMaster Class見ながら勉強したんですけどねw作り方はVOPネットワーク内でtabメニューから"if block"使い方。こんな感じ"Block Begin if"に条件の判定結果とFlaseの時の値、"Block End"に条件がTureの時の値を繋いで使う。"Block Be[...]
続きを読む -
MotionBuilder:Pythonコマンド
最近MotionBuilderのスクリプトを書くのですが、日本語の資料も少なく調べるのに手間取ったので、備忘録もかねてメモの一部公開します。確認環境はMotionBuilder2013です。MotionBuilderでPythonを書き始める際のとっかかりになれば幸いです。名前からオブジェクトを取得for i in FBSystem().Scene.Components: oObj = FBFindModelByName("Cube") print oObj.Name選択をクリア[...]
続きを読む -
AE:Tips02 (複数起動コマンド)
AfterEffects(以下AE)を複数起動する方法について。cmdで起動時にオプション "-m" で複数起動できます。下は参考例です。"C:\Program Files (x86)\Adobe\Adobe After Effects CS3\Support Files\AfterFX.exe" -mデスクトップ等のショートカットアイコンのリンク先に -m を追加すれば、cmdから実行しなくても済みます。AEのオプションはこれしか知らないのですが、他にもあるのでしょうか。[...]
続きを読む -
toxik:[Switcher]
toxikノード解説回です。今回はSwitcherです。名前の通り、切り替えるノードです。何を切り替えるのかというと、表示を、です。このSwitcherノード、入力が二つあります。PrimaryとSecondaryです。PrimaryにはImageが一つだけ、Secondaryにはいっぱいコネクトできます。これらのうち、Primaryに接続された方が表示されます。Switcherノードが持つパラメータはSelected Imageだけ。コレを切り替えることで、表示する画像を切り替えます。実際にやってみると、PrimaryとSecondaryの[...]
続きを読む -
Houdini:Wrangle Memo 03
Houdini回。Wrangle(SOP)のVEX例文。メモより抜粋その3。脈絡はないです。あと、時々コードが文字化けしてます。すいません。ローカル変数のマッピングi@test = 0;addvariablename(geoself(), "test", "TEST");自分で作ったアトリビュートをローカル変数として定義する。ここで定義したローカル変数は、このaddvariablenameという関数をサポートしたノードで利用可能らしい。最近の仕様では、あまりローカル変数使わないようになってるんだっけ[...]
続きを読む -
Maya:『Contour系ノード』 その2
前回に引き続きContourについてです。検証バージョンはMayaは2012の英語版です。より新しいバージョンでは設定が変更になっている可能性もありますのであしからず。Contourノードを使ってラインを描画する場合は次の手順で行います。(ここでは極力、Contourノードのみで設定する方法を紹介します)Contourノードは下の絵の赤枠内のノード群のことです。ではやっていきます。step1CustomShadersのContrastShaderに”contour_contrast_function_level"もしくは"contour_cont[...]
続きを読む -
Houdini:続・ベイクする
Houdini回。かなり前になりますがチャンネルのベイク方法について書いたのですが、CHOPのベイクがもっと簡単にできてたので備忘録も兼ねて。いつからだろ? もしかしてはじめからから? まぁ、よい。ベイク用に次のようなアニメーションを用意しました。箱がZ方向へ直進するアニメーションをキーフレームで作成して、それに対してCHOPでノイズを足したものです。キーフレームは最初と最後にのみ打ってます。この動きをベイクします。ベイクしたいチャンネルで右クリックメニューからを選択すると”Bake Keyframes on Selected[...]
続きを読む -
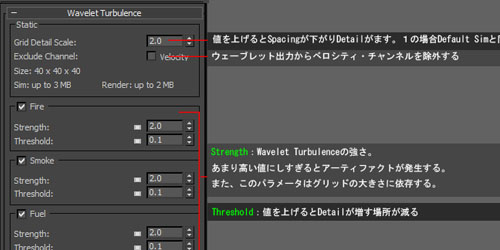
FumeFXメモ その5 [wtp]
FUmeFXのリファレンスメモ、5回目です。今回は、wtpタブの項目です。バージョンは3.5。Waveletは低解像度Gridで作成したものを、印象を変えずに高解像度に変換する手法です。Waveletの使用手順について1:Extra DetailにWaveleteをしてして普通にシミュレーション2:SimulationモードをWaveleteに変更する(シミュレーションボタンが変わる)3:Waveletの設定をする( Grid Detail Scale等)4:Waveletシミュレーションボタンを押す5:CacheをW[...]
続きを読む -
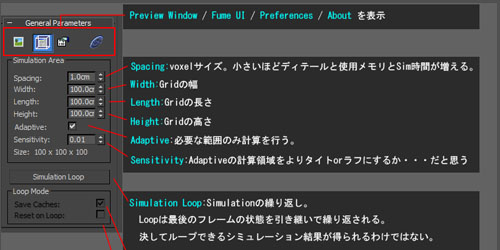
FumeFXメモ その1
3dsMaxの流体プラグインFumeFXのメモを今回から数回に分けて公開します。改めてまとめてみると、いろいろ発見があるものですね。今回は作成時のパラメータメモバージョンは3.5です。<General Parametersロールアウト><Viewport ロールアウト>●ショートカット: = FumeFX UIを表示する間違い等ありましたら、ご指摘いただけると助かります。その1 ?,その2 ,その3 ,その4 ,その5, その6, その7, その8, その9RayFireのパラメータ意訳メモ[...]
続きを読む